admin
La web de Maco048. Criminología
Las mentes simples casi siempre yerran en sus juicios
La paradoja del diablo
Esta es la paradoja del diablo:
Estás en el infierno, condenado para toda la eternidad. El diablo te ofrece una salida. Solo tienes que decidir qué día participar en una lotería en la que, si ganas, vas al cielo también para toda la eternidad y, si pierdes, te quedas como estabas, en el infierno para siempre jamás. El truco es que las probabilidades de ganar cambian cada día de la siguiente manera: si eliges que la lotería sea hoy la probabilidad de ganar es 1/2, si eliges que sea mañana pasará a ser 2/3, pasado mañana será 3/4, al día siguiente 4/5 y así sucesivamente. Como vemos, a medida que esperas la probabilidad de ganar aumenta. Permíteme que insista: la lotería es solo una vez, ganes o pierdas, ya no habrá más. Suponemos, habrá que decirlo, que el infierno te disgusta mucho (quema y eso) y el cielo te encanta (hay más atracciones aparte de estar tocando la lira).
La paradoja surge porque pareciera que siempre conviene esperar un día más. Por mucho que te disguste el infierno y te guste el cielo, esperar un día más supone estar un día en el infierno a cambio de un aumento de la probabilidad de estar infinitos días en el cielo. Por pequeño que sea este aumento, es un aumento y es por infinitos días. Claro que si siempre merece la pena esperar, entonces te quedas siempre en el infierno, cosa que tampoco quieres.
Fuente: Todo lo que sea verdad
Poincaré y el caso Dreyfus
Henry Poincaré es uno de los matemáticos franceses más notables del siglo XX, y tuvo una especial repercusión en el caso Dreyfus (Dreyfus affair). Comenzó en 1894 y finalizó en 1906. Tuvo una gran repercusión en Francia, donde sucedió.
El joven capitán Albert Dreyfus fue detenido y acusado de alta traición y trabajar para el enemigo. Su acusador fue el general Alphonse Bertillon, cuya prueba principal era una carta supuestamente manuscrita por Dreyfus y encontrada en la embajada alemana. A este documento se le conoció como la bordereau. Al principio el pueblo creó firmemente en la culpabilidad de Dreyfus, principalmente porque era descendiente de judíos e hicieron mucha prisión los grupos antisemitas de Francia (fuente).
Se convocó a tres expertos matemáticos para dar validez a la prueba pseudo-científica que elaboró Bertillon para asegurar que la bordereau fue escrita por Dreyfus. Acudieron al juicio Paul Appell, Gaston Darboux y Henri Poincaré. El último por entonces ya gozaba de una gran reputación internacional, y las conclusiones que redactó en un tono que no admitía contestación, zanjaron la polémica en torno a la autoría de la carta. A continuación, adjunto un extracto de traducción propia que Poincaré reflejó en alguna de sus cartas cuando le pedían la opinión sobre el sistema de Bertillon (fuente):
Bertillon afirma que ha encontrado 4 de 26 posibles coincidencias. Suponiendo que es 0,2 la probabilidad de encontrar una coincidencia aislada, Bertillon concluye que la probabilidad de encontrar 4 coincidencias es de 0,016. Falso. 0,016 sería la necesaria para encontrar 4 de 4 coincidencias, y en realidad, su cálculo debería ser de 0,7.
Artículo completo en: Idea secundaria
Sobre la falsa afirmación: Solo 85 personas tienen la misma riqueza que la mitad más pobre del planeta
Respuesta breve: NO.
Respuesta más larga y precisa: con los datos disponibles NO lo podemos saber, tampoco parece muy probable.
Respuesta aún más larga: es muy difícil que lo podamos saber.
La frase sale del informe del Oxfam GOBERNAR PARA LAS ÉLITES Secuestro democrático y desigualdad económica (y titulada así hasta en The Guardian, Oxfam: 85 richest people as wealthy as poorest half of the world):
La mitad más pobre de la población mundial posee la misma riqueza que las 85 personas más ricas del mundo.
Actualización: En [Enlace bloqueado por la Tasa española AEDE].
Ampliar en: Ricardo Galli, de software libre
Autopsias verbales en India
La muerte en La India es un asunto privado. El epidemiólogo Prabhat Jha y otros investigadores llevan años luchando porque la situación cambie y los millones de muertes que se producen en el país, muchas en remotas aldeas, aparezcan en algún registro público. Un programa estatal bautizado como el Estudio del Millón de Muertes (Million Death Study) pretende documentar las muertes producidas entre 1997 y 2013 mediante encuestas personales a un millón de individuos. Hasta el momento llevan realizadas 450000 y los primeros datos están sirviendo para trazar un mapa de la mortalidad en el país que ya se está utilizando para cambiar la política sanitaria.
Los esfuerzos por documentar las causas de las muertes están dando sus primeros frutos. La revista Nature publicaba hace unos días una serie de gráficos ilustrando los niveles de incidencia de distintas enfermedades por regiones. El proceso consiste en la visita sobre el terreno de unos 900 encuestadores que acuden a distintos lugares del país para preguntar por la causa de muertes no registradas. Con los datos obtenidos, dos médicos analizan cada caso y concluyen esta denominada “autopsia verbal” que determina la causa de la muerte.
Se calcula que el 75% de las 60 millones de personas que mueren cada año en el mundo lo hace en países como La India en los que la causa de la muerte no se contabiliza de forma precisa. La Organización Mundial de la Salud (OMS) basa sus datos en la información obtenida de los hospitales, pero el resultado está muy distorsionado en lugares donde la gente muere lejos de un centro médico y las causas son invisibles para la estadística. Gracias al programa de encuestas, por ejemplo, las autoridades sanitarias indias han comprobado que la muerte por causas relacionadas por el tabaco es mayor de lo estimado y han endurecido sus campañas de prevención.
Aún así, el método de “autopsias verbales” ha sido cuestionado por algunos especialistas, que creen que el análisis estadístico puede ser más preciso y menos costoso. Hace dos años, un estudio publicado en The Lancet destacaba la espectacular diferencia entre la estimación de muertes por malaria de la OMS y el de la encuesta del millón de personas. Mientras que la OMS calculaba que cada año mueren unas 30000 personas por esta enfermedad, el cálculo de las autopsias verbales se disparaba por encima de las 200000 muertes. ¿Dónde estaba el problema?
Artículo completo en: CUADERNO DE CULTURA CIENTÍFICA
Dos físicos aseguran que el manuscrito Voynich contiene «un mensaje», y un lingüista lo niega
Dos físicos sostienen, en el último número de la revista PLOS One, que el manuscrito Voynich, que data del siglo XV, contiene un mensaje real y no es un cúmulo de signos sin sentido, cmo se creía hasta ahora. Después de someter el texto a análisis estadístico, Marcelo Montemurro y Damián Zanette concluyen que “presenta una organización compleja en la distribución de las palabras que es compatible con aquéllas existentes en lenguajes reales” y aseguran haber encontrado redes semánticas. “Estos resultados, junto con algunos rasgos estadísticos previamente conocidos del manuscrito Voynich, apoyan la presencia de un mensaje genuino en el libro”, sentencian.
Sin embargo, el lingüista y psicólogoGordon Rugg, experto en el texto y que en 2003 concluyó que no es nada más que un fraude, ha salido al paso inmediatamente, en la web de la revista y en su blog, diciendo que “hay algunos malentendidos desafortunados en este trabajo que afectan a sus conclusiones”. Destaca que “el hecho de que el texto del manuscrito Voynich no sea aleatorio es algo conocido desde hace tiempo” y que es “completamente erróneo” pensar que eso invalida la hipótesis del fraude, ya que las peculiaridades estadísticas descubiertas por los dos físicos serían un efecto no intencionado de cómo se perpetró el engaño.
Artíulo completo en: Magonia
Las probabilidades matemáticas de que lo de la infanta sea “un error”
Supongamos que ha sido un error humano. Supongamos que en realidad han sido cuatro errores humanos consecutivos e independientes, uno detrás de otro y por parte de personas sin relación entre sí: cuatro registradores de la propiedad distintos que tramitaron esas 13 falsas ventas del enredo de la infanta y que enviaron el DNI de Cristina de Borbón a la base de datos de Hacienda por error. De entre unos 46 millones de DNIs españoles, los cuatro se confundieron y escribieron precisamente el de la mujer de Iñaki Urdangarín. ¿Qué posibilidades habría en el universo de que ocurriese una casualidad así? La probabilidad de que se equivoquen los cuatro registradores y escriban por error, al azar, el DNI de la infanta es del orden de uno entre un 10 seguido de 30 ceros. Es decir: una entre 10.000.000.000.000.000.000.000.000.000.000. O lo que es lo mismo, una entre diez quintillones. Una posibilidad entre diez billones de trillones.
Más números grandes y probabilidades pequeñas. Si en lugar de cuatro, se hubieran equivocado diez eligiendo precisamente el DNI de la infanta –entre registradores y notarios–, tal coincidencia sería matemáticamente tan probable como la de elegir por azar precisamente un átomo en concreto entre todos los del universo (una cifra con 79 ceros).
Para ser justos con la infanta y con la torpeza de los registradores imaginemos que el número posible de DNIs parecidos al de su alteza fuera sólo de 100; no mucha gente tiene un carné de identidad VIP de solo dos dígitos. Incluso así, la probabilidad de que los cuatro registradores se hubiesen equivocado y escribiesen por azaroso error el número de la infanta sería de una entre 100 millones. O lo que es lo mismo, aproximadamente una entre dos veces el «bárcenas», ese gran número recién descubierto en Suiza y que equivale a unos 47 millones.
Por comparar, la probabilidad de que te caiga un meteorito en la cabeza es solo una entre 174 millones. Si yo fuese esa anomalía estadística llamada Cristina Federica Victoria Antonia de la Santísima Trinidad de Borbón y Grecia, me pondría casco.
Y si yo fuera Cristóbal Montoro buscaría una excusa mejor. Una que no insulte la inteligencia de cualquier contribuyente español.
- José Manuel Rey, coautor de este artículo y quien ha hecho los números, es doctor en matemáticas y profesor de la Universidad Complutense de Madrid.
Fuente: elDiario.es
Licencia CC
Anexo: en magnetotrouble publican una corrección al contenido anterior, denominada P-valores, infantas y tests de hipótesis
Probabilidad de morir por impacto de un asteroide
La probabilidad de que una persona muera por impacto directo de un asteroide se ha calculado en 1 entre 74817414, . Comparativamente la probabilidad de que acertar todos los números de los Euromillones es de 1 entre 117 millones más o menos. En otras palabras: es más fácil que te caiga el pedrolo encima el viernes por la noche a que llegues multimillonario al sábado.
Fuente: National Security Council / The Economist
Sherlock Holmes y una bicicleta
En uno de los relatos cortos de Sherlock Holmes “La aventura del colegio Priory”, una de las claves para resolver el misterio es decidir en qué dirección viajaba una bicicleta. Así cuando Watson plantea que puede venir en cualquiera de las dos direcciones, Sherlock le contesta:
“- No, no, querido Watson. La impresión más profunda es, naturalmente, la
de la rueda de atrás, que es donde se apoya el peso del cuerpo. Fíjese en que
en varios puntos ha pasado por encima de la huella de la rueda delantera, que
es menos profunda, borrándola. No cabe duda de que venía del colegio.
Puede que esto tenga relación con nuestra investigación y puede que no, pero
lo primero que vamos a hacer es seguir esta huella hacia atrás.”
Naturalmente Sherlock tenía razón en dos cosas: normalmente la rueda de atrás soporta más peso y la trazada de la rueda trasera puede pasar por encima de la delantera y no a la inversa. Pero lo que no está tan claro es que si tenemos las huellas dejadas por las dos ruedas de una bicicleta seamos capaces de determinar el sentido en el que viajaba ella, salvo si existen otros tipos de huellas como salpicaduras que marcan siempre como una flecha la dirección en que nos movemos.
Sin embargo, si los conocimientos de Sherlock Holmes (o de Arthur Conan Doyle) en matemáticas hubieran sido mayores, sí que se puede determinar con total precisión no sólo el sentido en el que se desplaza una bicicleta, sino algunas de las dimensiones de esta.
El caso se resuelve matemáticamente en «Mati, una profesora muy particular», usado los siguientes elementos:
1) La rueda que marca la dirección es siempre la rueda delantera, la trasera no hace sino seguirla a ella. Esto es: en cada punto, la rueda trasera (o el plano imaginario en el que se encuentra dicha rueda), apunta hacia el punto en el que la rueda delantera toca al suelo.
2) Si intersecamos el plano que define cada rueda con el suelo obtenemos una recta para cada una de las ruedas en cada momento.
3)Y (éste es el punto clave y un poco más delicado) cada una de las rectas que hemos mencionado en 2) ha de ser tangente con la curva que define el trazado de la rueda.
A partir de 1, 2 y 3 se puede ver claramente, y ésta es la clave, que: la tangente a la curva que describe la segunda rueda corta a la curva que describe la primera rueda y la longitud del segmento de tangente entre ambas curvas es siempre el mismo (la distancia entre las dos ruedas).
Argumentación y lógica
Taller de argumentación y lógica básica de la Asociación Escéptica de Chile
Vídeos (VOD) del taller
Watch live streaming video from talleraech at livestream.com
Watch live streaming video from talleraech at livestream.com
Watch live streaming video from talleraech at livestream.com
Watch live streaming video from talleraech at livestream.com
Diapositivas de las presentaciones
Diapositivas de la sesión 1.
Diapositivas de la sesión 2.
Diapositivas de la sesión 3.
Diapositivas de la sesión 4.
Fotografías tomadas durante los eventos
Sesiones 1 y 2:
Asociación Escéptica de Chile
Contenido con copyright de sus autores al año de publicación, licenciado bajo una licencia Creative Commons Atribución-NoComercial-CompartirIgual 3.0 Chile (CC BY-NC-SA 3.0)
Cuestión sencilla que casi nadie responde correctamente
El cerebro humano es el órgano más complejo que se conoce y es el producto de la evolución a lo largo de millones de años. El cerebro, por su funcionamiento interno, necesita siempre asignar una causa concreta a una acción determinada, sin embargo, suele fallar cuando no existe una causa determinada, es decir, falla cuando el azar es el protagonista. El problema es que el azar es una parte fundamental de la naturaleza y está presente en todas partes y en todas las facetas de nuestra vida: economía, deportes, trabajo, política, etc. Esto da lugar a que en una gran cantidad de situaciones cometamos flagrantes errores: médicos que sobreestiman (o subestiman) enormemente las posibilidades reales de tener graves enfermedades, políticos que sobreestiman las posibilidades de éxito de sus medidas, empresas que sobreestiman la verdadera capacidad de generar riqueza de sus directivos, guiones de películas o novelas potencialmente millonarias que son rechazadas por los editores, inocentes que pasan años en la cárcel por que abogados, jueces y jurado no interpretaron correctamente las estadísticas y subestimaron las posibilidades de que un violador vuelva a actuar…
Concurso millonario
Estás participando en un concurso cuyas reglas son muy simples: hay tres puertas, en dos de ellas hay una docena de libros de recetas de cocina y en una de ellas hay un coche Ferrari. Elige una de ellas, a continuación el presentador abre una de las otras dos puertas y muestra los libros de cocina. Después pregunta: ¿Quiere cambiar su elección y escoger la otra puerta que falta o mantiene su elección inicial? ¿Que harías, cual es la opción con más probabilidades?
La respuesta a esta pregunta es una de las impactantes en cuanto a que nuestra intuición nos dice inmediatamente que la respuesta es obvia: no hay ninguna diferencia entre mantener la elección o cambiar la puerta, obviamente las posibilidades de acertar son del 50%. Pero esto es ¡FALSO! Para darnos cuenta que casi nadie es capaz de responder correctamente a esta pregunta (nadie que no la haya oído y entendido de antemano) esta pregunta fue formulada a uno de los matemáticos más importantes de los últimos años: Paul Erdos y respondió de forma incorrecta (dijo que las probabilidades eran del 50%), incluso cuando se le mostró la respuesta afirmó «esto no puede ser correcto» y solo se convenció cuando se le mostraron los resultados de simulaciones numéricas del problema en un ordenador.
La respuesta es que tienes el doble de probabilidades de ganar el Ferrari si cambias de puerta. Es decir, si te mantienes en tu elección inicial las probabilidades de éxito son solo de 1/3 o del 33% sin embargo, si cambias, las probabilidades de ganar son de 2/3 o del 66%. Esto, sin explicación, es muy difícil de creer así que vamos a explicar el porque con detalle.
Existen dos escenarios posibles:
Escenario 1: La elección inicial es la correcta. En este caso la puerta que eliges al principio es la que esconde al Ferrari por lo que cambiar de puerta después siempre tendrá como consecuencia perder el Ferrari. Este escenario tiene claramente 1/3 de probabilidad de ocurrir.
Escenario 2: La elección inicial es incorrecta. En este caso el Ferrari está detrás de una de las dos puertas restantes. En este caso sucede algo muy importante a diferencia del caso anterior: el presentador no va a abrir una puerta cualquiera, va a abrir una de las dos puertas restantes, precisamente la que no esconde el Ferrari por lo que la puerta que no ha abierto ¡Es la que esconde el Ferrari! De forma que en este escenario cambiar de puerta siempre tendrá como consecuencia ganar el Ferrari y este escenario ocurre 2/3 de las veces.
Por tanto la respuesta es que cambiando de puerta tienes el doble de posibilidades de llevarte el Ferrari.
En la televisión han existido programas de este tipo y las estadísticas muestran claramente que aquellos concursantes que cambian de puerta, de media, ganan el doble de veces el concurso que los que no lo hacen.
Este ejemplo muestra también que el cálculo de probabilidades es algo que puede ser muy sutil y delicado, ya que hay que analizar muy bien la información disponible y analizar con cuidado el papel de la aleatoriedad. En este ejemplo la aleatoriedad ejercida por el presentador es distinta en ambos escenarios: en el escenario uno cualquiera de las puertas que abra no contiene el Ferrari por lo que esta acción no influye en el hecho de que cambiar de puerta siempre conlleva perder, sin embargo, en el escenario dos el presentador ayuda al concursante eliminando la puerta que no tiene el Ferrari e indicando al concursante cual es la puerta ganadora.
Fuente: El andar del borracho, 2008. Leonard Mlodinow
Algoritmo que puede ayudar a identificar la fuente de crímenes, epidemias y rumores
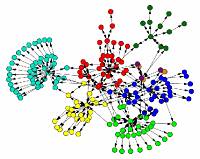
Seguir un acto delictivo o un rumor hasta su origen puede ser muy complicado a veces, más en estos tiempos donde una red criminal puede tener innumerables nodos, ramificaciones y caminos, formando grafos realmente complicados de analizar y descubrir su origen. Por ello, Pedro Pinto, del Laboratorio de Comunicaciones Audiovisuales y sus colegas se pusieron manos a la obra, desarrollando un algoritmo que podría ayudar a resolver problemas en los que se vea involucrada una red.
El algoritmo logra identificar la fuente de cualquier tipo de cosas que circulen por una red simplemente “escuchando” un número finito de miembros que componen esa red. El ejemplo práctico que Pinto pone es:
Imagina que te encuentras con un rumor sobre ti en Facebook que se ha extendido por 500 de tus amigos. Sólo con mirar los mensajes recibidos por 15 de tus amigos y teniendo en cuenta el tiempo, nuestro algoritmo puede descubrir el camino de vuelta y encontrar la fuente.
En cuanto a la identificación de orígenes de crímenes, es más complicado hoy en día que en las mafias organizadas de los años 50, donde existía una estructura organizada que podía formar, más o menos, una estructura de árbol; sin embargo, el algoritmo fue aplicado con éxito en la identificación de los criminales relacionados con el 11 de septiembre o en casos de ataques a estaciones subterráneas, como el atentado en Tokyo de 1995, donde se liberó gas tóxico en las estaciones.
Fuente: Faltaría más
El héroe olvidado y condenado injustamente, Alan M. Turing
En la navidad de 1951, Alan Turing entabló amistad con Arnold Murray, un joven desempleado de Manchester de 19 años de edad que se convertiría en su amante y con el que conviviría. A principios de 1952 se produjo un robo en su casa, realizado por un amigo de Arnold, que Turing denunció a la policía. Por supuesto, sin revelar su relación homosexual, irrelevante al caso. Cuando la policía averiguó la historia completa, dejó de interesarse por el robo, que nunca fue resuelto, y m0stró un mayor interés por los encuentros sexuales de Turing, procediendo a su arresto por homosexualidad, una “práctica” entonces considerada como delito y como enfermedad.
Fue acusado, los cargos que le fueron imputados eran de “indecencia grave y perversión sexual“, los mismos por los que en su día ya fuera condenado Oscar Wilde años atrás. El juicio del caso “la Reina contra Turing y Murray” tuvo lugar el 31 de marzo de 1952, presidido por el juez J. Fraser Harrison. En la corte, Turing, contraviniendo las recomendaciones de sus amigos, no negó su homosexualidad, y sostuvo que no había nada malo en ella, convencido como estaba que no tenía nada por lo que disculparse. Así pues, Turing no se defendió de los cargos y su único alegato se limitó a insistir en que él no había hecho nada malo. Efectivamente, las recomendaciones eran fundadas, pues el fiscal aprovechó ese alegato para enfatizar la “falta de arrepentimiento” del acusado.
Fue condenado, privado de sus derechos ciudadanos, y se le dio la opción de escoger: o como delincuente ser condenado a un año de prisión, o como enfermo someterse a un tratamiento hormonal para la reducción de la libido y “curar” su homosexualidad, lo que en realidad era una auténtica “castración química”. Finalmente, y para su desgracia, escogió las inyecciones de estrógenos, hormonas femeninas, en un tratamiento brutal que duró un año, y que le produjo importantes alteraciones físicas, como la aparición de pechos, le convirtió en impotente y le provocó una profunda depresión que no pudo o no quiso superar, tras la injusticia de que estaba siendo objeto. Solitario, raro e imprevisible, nervioso y comiéndose las uñas, más frustrado y desesperado que nunca por su mala forma física, artificialmente inducida por una justicia mojigata y absurda, con el añadido de la exasperante vigilancia policial de que todavía era objeto, así como el abandono de algunos de sus supuestos amigos, Turing decidió que no valía la pena seguir viviendo. Dos años después del juicio, el siete de junio de 1954, murió, al comer de una manzana envenenada con cianuro. La muerte fue calificada como suicidio. Contaba apenas con 42 años.
Ampliar en: HABLANDO DE CIENCIA
